How to Convert Octal to Binary

Octal to Binary

In mathematics, there are different number systems to write numbers, say binary number system (base 2), octal number system (base 8), decimal (base 10), and hexadecimal number system (base 16). Octal to binary conversion is defined as converting a number from base-8 to base-2. It can be done in two ways that you will learn in this article. Let us move ahead and learn the conversion of octal to binary.

☛You may need this online tool: Octal to Binary Converter

What is Octal to Binary Conversion?

Before learning about octal to binary conversion, let us quickly go through the meanings of the octal number system and binary number system. The binary number system uses only two digits 0 and 1 to represent numbers. It is also known as the base-2 system. It is used with the computer system in which 0 and 1 digits are used to write various scripts. Each digit i.e. either 0 or 1 is referred to as a bit in the binary system. For example, (01101)₂, (01000010)₂, (11000101)₂ are a few binary numbers. On the other hand, the octal number system includes digits from 0 to 7. Other digits like 8 and 9 are not included in this system. It is also known as the base-8 system. Just as the binary, the octal number system is used in minicomputers. For example, (73)₈, (151)₈, (35)₈ are a few octal numbers.

Conversion of octal to binary is defined as converting a number from base-8 to base-2 by using either direct or indirect methods. All the digits in an octal number are from the range of 0 to 7, while all the digits in a binary number include only 0 and 1. Let us observe the octal to binary table given in the next section.

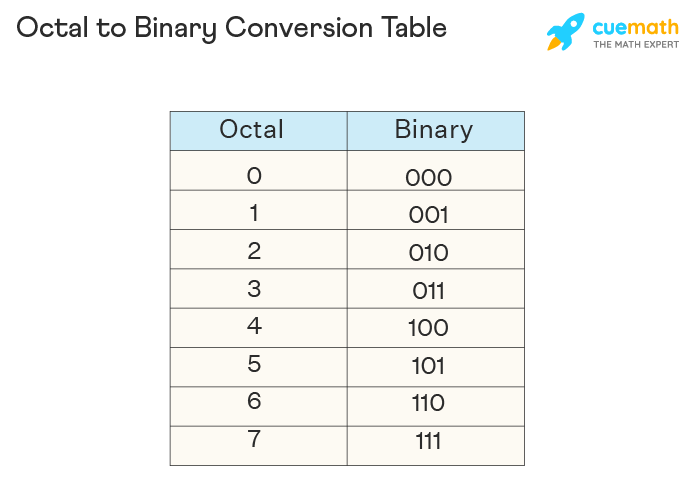
Octal to Binary Table

Observe the octal to binary table given below which will help you to convert octal numbers to binary numbers. The octal to binary table shows the equivalent number of each octal digit to binary, for example, 0 in octal is equivalent to 000 in binary, 1 in octal is equivalent to 001 in binary, 2₈ is the same as 010₂, and so on.

How to Convert Octal to Binary

There are two ways to convert octal to binary, which are explained below:

• Convert octal to decimal and then decimal to binary
• The direct method of octal to binary conversion

Let us understand each method in detail one by one.

Method 1: Octal to decimal and then decimal to binary

In this method, we will first convert a number from octal to decimal (base 10), and then we will convert that decimal number to binary. To convert a number from octal to decimal, we multiply its digits starting from the right with 8 raised to exponents starting from 0 and then add the values. So, the first digit from the right will be multiplied by 8⁰, which is equal to 1, the second digit will be multiplied by 8¹ = 8, and so on.

Let us take an example of the number 56₈. The 8 written as the base represents that this is a base-8 number. 56₈ can be converted to base 10 as,

56₈ = 6 × 8⁰ + 5 × 8¹

56₈ = 6 × 1 + 5 × 8

= 6 + 40

= 46

Hence, 56₈ = 46₁₀. Now, we will convert 46 which is a base 10 number to its binary equivalent. To convert decimal to binary, divide the given number by 2 and note down the quotient and reminder. Again divide the quotient obtained by 2, and note down the remainder. Repeat this process till you get 0 as the quotient. Write the remainders in order from right to left. Let us convert 46₁₀ to binary.

Divide 46 by 2 ⇒ 46 ÷ 2 = Quotient - 23, remainder - 0

23 ÷ 2 = Quotient - 11, remainder - 1

11 ÷ 2 = Quotient - 5, remainder - 1

5 ÷ 2 = Q - 2, R - 1

2 ÷ 2 = Q - 1, R - 0

1 ÷ 2 = Q - 0, R - 1

Arrange all the remainders from right to left. We will get,

46₁₀ = 101110₂

Therefore, we have converted an octal number 56₈ to its binary equivalent 101110₂.

Method 2: Direct Method of Octal to Binary Conversion

Another method, surely an easier and less complicated one, is to directly convert a number from octal to binary by referring to the octal to binary table given above. In this method, we convert every digit of the given octal number to its binary equivalent by referring to the above chart. For example, using this method we can directly write 3₈ as 011₂, 5₈ as 101₂, etc.

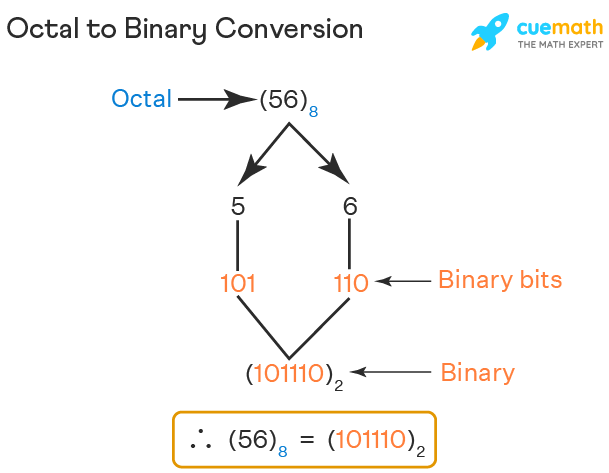
Let us convert the same number 56₈ from octal to binary using the direct method. There are two digits in this number, 5 and 6. Referring to the above octal to binary chart:

5₈ → 101₂

6₈ → 110₂

By combining these two, we will get, 56₈ = 101110₂. Observe the image given below for your reference.

Octal to Binary Example

 

Example : Convert the octal number 72₈ to a binary number using the decimal conversion method.

Solution: Given octal number 72₈. To convert it to a binary number using the decimal conversion method, we will first convert it to a decimal number.

⇒ 72₈ = 2 × 8⁰ + 7 × 8¹

⇒ 72₈ = 2 × 1 + 7 × 8

= 2 + 56

= 58₁₀

Now, we have to convert 58₁₀ to a binary number by repeatedly dividing it by 2.

⇒ 58 ÷ 2 = Q - 29, R - 0

29 ÷ 2 = Q - 14, R - 1

14 ÷ 2 = Q - 7, R - 0

7 ÷ 2 = Q - 3, R - 1

3 ÷ 2 = Q - 1, R - 1

1 ÷ 2 = Q - 0, R - 1

We get, 58₁₀ = 111010₂. Therefore, the octal to binary conversion of the number 72₈ results in 111010₂.